【48812】轮船渡河问题常识整理新东方在线教你怎么回答运动的组成与分化

  “轮船渡河”是高中物理中有关运动组成与分化的典型问题，因其在解题进程中往往还会涉及到受力剖析及分类评论，所以一直是高考物理的难点地点。

  新东方在线教师指出，运动的组成与分化是高中物理中使用极端广泛的一种解题剖析技巧，把握此类剖析办法，能够显着提高解题功率。今日，新东方在线教师就对“轮船渡河”两大常考题型进行深度整理回答，期望有时机能够协助同学们全面把握。

  常理来看，想要“轮船渡河”位移最短，依据“两平行线笔直间隔最短”的定理，此刻轮船渡河位移间隔刚好等于两岸河边的宽度。但是，轮船渡河时并不会以笔直方向径自开往河畔彼岸，轮船在必定流速的水中渡河时，实践会参加两个分运动进程，即流水速度和轮船的静水速度，所以轮船实践行进的轨道应该是两个运动的合运动轨道。此刻，当轮船合速度笔直于岸边时，渡河位移最短。

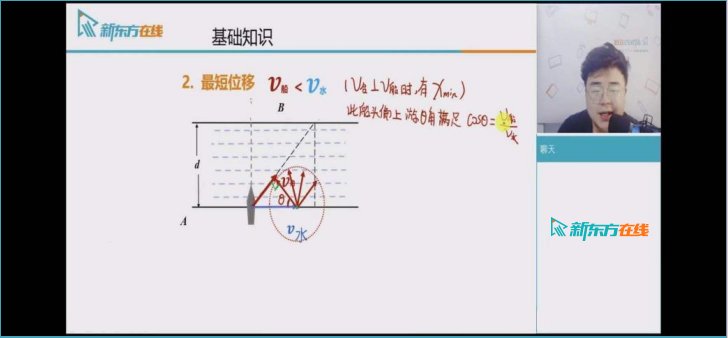
  除此之外，同学们在回答此类问题时，要最大极限地考虑两种状况，一是当轮船速度大于流水速度时，合速度方向笔直于河边，此刻最短位移就为河边宽度。二是若轮船速度小于流水速度时，轮船运动轨道无法笔直于河边，同学们就需求保证轮船速度笔直于合速度方向，此刻实践轨道偏转的视点最小，则轮船实践渡河位移也最短。

  因而，同学们在遇到位移最短类问题时，要先受力剖析找出水流、轮船、实践速度（合力）的方向，然后依据题干问题，去选定条件。判别轮船速度与流水速度巨细，进行分类评论，解出终究答案。

  “轮船渡河”时刻问题相对位移问题较为简略，若想坚持轮船实践渡河时刻最短，则只需求坚持轮船船头彻底笔直河边行进即可。依据“时刻等于间隔除以速度”，此刻合力轨道尽管不笔直于河边，但当船头笔直于河边时，此刻轮船速度到达最大值，因而全体渡河时刻最短，而且整一个完好的进程中，轮船渡河时刻并不遭到静水速度的影响。

  新东方在线教师指出，同学们在回答“时刻最短”和“位移最短”两类题型时，首要都需求依据条件来进行作图，先画静水速度（从始至终坚持河边平行），然后依据条件画出轮船速度，最终依据合力速度确认轨道方向，这样的一整套剖析愈加科学，也更明晰明晰。

  “轮船渡河”问题圈套较多，同学们需求在平常操练时做好基础训练，充沛剖析已知条件寄问题问法，在此基础上才干真实深度把握运动的组成与分化问题。除了以上内容，同学们也能够下载新东方在线APP或许登录官网向教师咨询讨教。